AVL Tree
A “generic” AVL Tree, from the dark days before templates… The code here is some of my first C++. Back in 1991 C++ was still pretty new. Looking back at my early C++ is better than looking back at my early C. At least my early C++ just looked like OKish C with some odd keywords…
How do you index a data structure that keeps changing?
The game world for the multi-user adventure system I was writing between ‘89 and ‘94 was stored in a network of interconnected nodes. I called it a Semantic network because of some AI book I’d read at the time, the whole of the knowledge of the game world was in this network. The design of the game meant that people could create new objects or rooms via magical powers, alternatively they completely remove items from the world. Because of this dynamic nature of the world itself the index into the world needed to be able to handle regular inserts and deletes without degenerating… I remember reading about AVL trees in the Turner Simms concert hall at Southampton University whilst watching my girlfriend rehearse (Data Structure Techniques - Standish - 0-201-07256-4 page 108…). I decided that they sounded like the ideal index into my network. I planned to have some form of trie index at the top level with AVL trees below each letter…
What’s an AVL tree then?
AVL trees, named after the Russians, Adel’son-Vel’skii and Landis, who first defined them, are height balanced binary search trees. To be considered an AVL tree a binary search tree must satisfy only one condition: for any node, the height of the left sub-tree and the height of the right sub-tree must differ by no more than one. As nodes are added and removed one or more node may lose the AVL property and need to be re-balanced. This can be achieved by applying one of four “rotations”, this is far more efficient than having to reorganise the whole tree as you would to keep a binary tree perfectly balanced. In the worst case, a search for a specific node in an AVL tree will require 45% more comparisons than a perfectly balanced binary search tree. Whilst in the average case the additional comparisons required are negligable.
The four rotations…
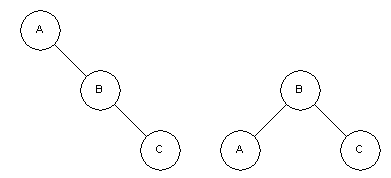
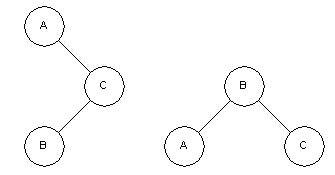
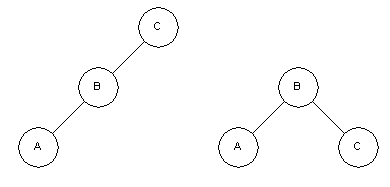
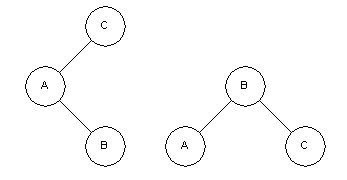
In all of the diagrams below the node “A” is being examined for the AVL property and requires a rotation to restore it. Each rotation will return node “B” which will have been adjusted so that it meets the requirements of the AVL tree.
Rotate left
Double rotate left
Rotate right
Double rotate right
Additions of nodes deep in the tree can cause a cascading series of rotations all the way back to the root. This can be clearly seen from the test harness.
An ideal “learning C++” project… (pity I didn’t really use C++)
Since I was learning C++ at the time I decided to implement the index in C++ (I later converted it to C for the Unix port of the game…). Having written it I wanted to be able to store all manner of things in it, so I made it “generic”. At the time the best I could do was tell the tree how big the items you were storing were and supply a comparison function. The compiler of the day didn’t support templates but why my generic datatype of choice was a BYTE * rather than a void * I don’t know. What scares me now is looking at the code and seeing how huge the member functions are and how much is going on. There’s no use of abstraction to make things easier to understand, nothing’s broken into easily digested chunks. There’s lots of comments though, so it must be good ;). Also I really disliked those C++ stream things, lets stick with printf() it’s nicer…
I can’t remember why I use the complicated stack based method of traversing the tree. I know I wrote a version which used recursion but I think I managed to blow the stack when testing it on DOS and so switched to a method that wouldn’t blow the stack…
I’d just read about using gotos to get out of horrible error situations and was trying it out. Though I believe the technique of using multiple gotos to jump to a single clean up point on error is OK I wouldn’t use it often today.
I remember playing for hours with this looking for a bug that I don’t recall ever finding (can’t think why, when the code’s so easy to read…) I seem to recall that the tree became unlinked once or twice and lost some nodes…
The test program adds letters to a tree and displays the tree as it dynamically balances. It’s cute to watch.
I might sit down and write a template version that uses recursion rather than the stack climbing method employed here. We’ll see.
Faster than it used to be…
Having just downloaded and run this code for the first time in forever I notice that it runs a little too fast on modern hardware. Adding the following slows it down to something that you can see…
In the code that looks like this:
#include < math.h > // pow
#include < dos.h > // sleep
#include < time.h > // time
int count;
int compChar(BYTE *itemOne, BYTE *itemTwo)
Add this:
#include < math.h > // pow
#include < dos.h > // sleep
#include < time.h > // time
#include < Windows.h > // <----
int count;
int compChar(BYTE *itemOne, BYTE *itemTwo)
And in the code that looks like this:
//count++;
if (count == 10) {
fprintf(stdout,"\n%s\n",dispBufPtr);
count = 0;
}
printf("\n%s\n",dispBufPtr);
delete dispBufPtr;
}
#endif
Add this:
//count++;
if (count == 10) {
fprintf(stdout,"\n%s\n",dispBufPtr);
count = 0;
}
printf("\n%s\n",dispBufPtr);
delete dispBufPtr;
::Sleep(500); // <----
}
#endif
Download
The source was originally built with Borland C++ v3.1 but it compiled up straight away on VC++ v5.0.

